騒音の距離減衰式の解説

はじめに

音は距離が離れるにしたがって小さくなります。
発生源の騒音レベルが分かっていれば、計算式によって受音点の騒音レベルが予測できます。
今回はこの予測式について解説していきたいと思います。

参考までに騒音・振動・低周波音でお悩みの方は以下の動画も参考にして下さい。

音源の種類

発生源の音には点音源、線音源、面音源と3種類あります。
この音源の種類によって予測式を使い分けていきます。

• 点音源
  音源と小さい場合
  音源と予測点の距離が離れている場合
  発生源が点在している場合
• 線音源
  音源が長い場合
  道路など
  道路交通騒音などを予測する場合
• 面音源
  音源が大きい場合
  音源と予測点が近い場合
  工場の壁面などの近くで予測する場合

点音源の予測式

騒音の予測をする場合、点音源と予測することがほとんどであると考えられます。
倍距離で6デシベルの減衰です。

予測式は以下の通りになります。

10m（SPLr0=100として）
　SPLr＝100-20log((10/1)=80.00dB

20m（SPLr0=100として）
　SPLr＝100-20log((20/1)=73.98dB

線音源の予測式

線音源の予測式は2つに分けられます。
ほとんどの場合は倍距離で3デシベルの減衰です

音源が長い線状の場合

長い道路の音を離れた場所で予測する場合に用います。

10m（SPLr0=100として）
　SPLr＝100-10log((10/1)=90.00dB

20m（SPLr0=100として）
　SPLr＝100-10log((20/1)=86.99dB

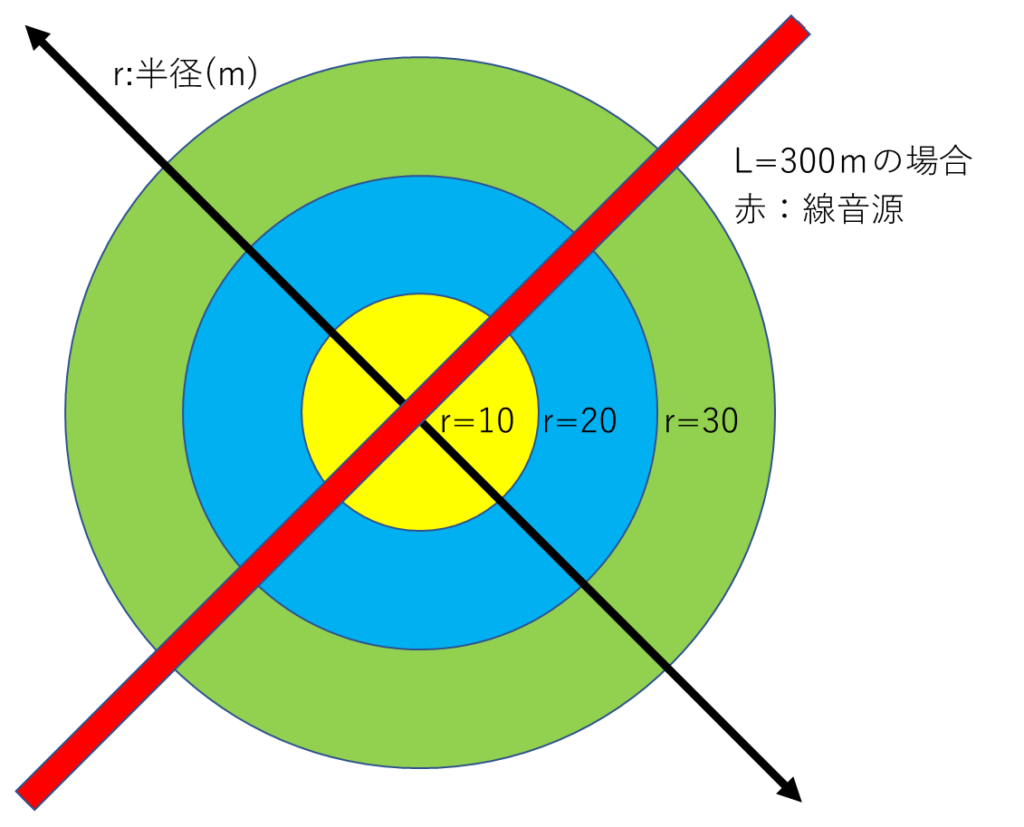
音源が有限な線状の場合

工場などで音源が横に一直線に並んでいる場合を想定します。

96m（SPLr0=100として）
　SPLr＝100-10log((300/3.14)/1)-20log(96/(300/3.14)=80.16dB

192m（SPLr0=100として）
　SPLr＝100-10log((300/3.14)/1)-20log(192/(300/3.14)=74.14dB

例）
〇ｍ地点はどっちの式？
r≦L/π
10m地点は？
10≦300ｍ/10m
10≦30
　①の式
r≧L/π
96m地点は？
　96≧300m/3.14
　96≧95.54
　②の式

ほとんどの場合は①の式が適用される。
線音源の場合、距離が2倍離れると3dB減衰する。

面音源の予測式

面音源は基本的には減衰しません。
距離によって適用される式が少しずつ変わります。

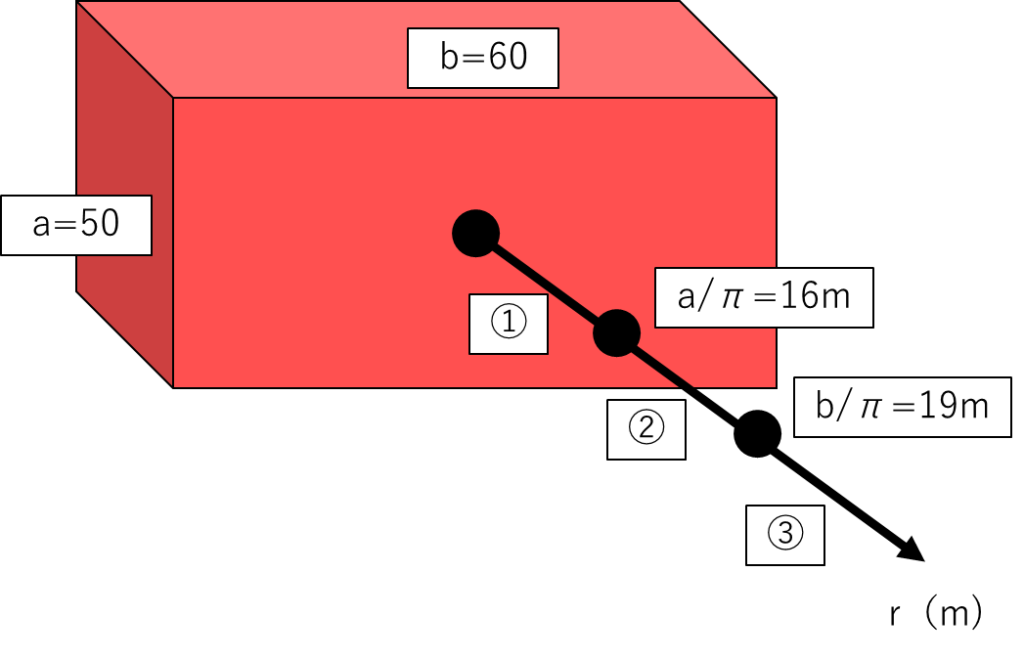
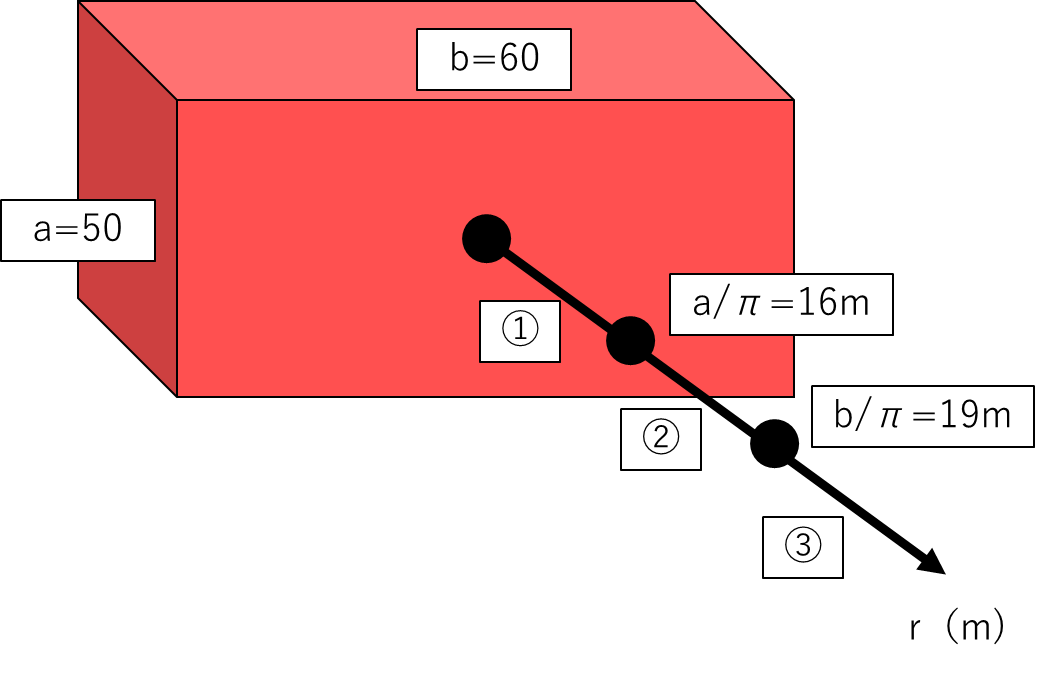
例）
壁面がa=50ｍ,b=60mの場合
16mまでは①に該当し、騒音は距離減衰しません。
16m～19mは②に該当し、線音源と同じ減衰になります。
19m以降は③の式が該当します。

16mまで減衰なし

16m（SPLr0=100として）
　SPLr＝100-10log(16/(50/3.14))=99.98dB

19m（SPLr0=100として）
　SPLr＝100-10log(19/(50/3.14))=99.23dB

19.1m（SPLr0=100として）
　SPLr＝100-10log((60/3.14)/(50/3.14))-20log(19.1/(60/3.14))=99.21dB

30m（SPLr0=100として）
　SPLr＝100-10log((60/3.14)/(50/3.14))-20log(30/(60/3.14))=995.29dB

50m（SPLr0=100として）
　SPLr＝100-10log((60/3.14)/(50/3.14))-20log(50/(60/3.14))=90.85dB

60m（SPLr0=100として）
　SPLr＝100-10log((60/3.14)/(50/3.14))-20log(60/(60/3.14))=89.27dB

120m（SPLr0=100として）
　SPLr＝100-10log((60/3.14)/(50/3.14))-20log(120/(60/3.14))=83.25dB

180m（SPLr0=100として）
　SPLr＝100-10log((60/3.14)/(50/3.14))-20log(180/(60/3.14))=79.28dB

最後に

今回は騒音の距離減衰式についてまとめてみました。
実際の計算例も更新して行きたいと考えています。