はじめに
今回は振動について解説していきます。
振動って何ってところから、揺れの大きさまで換算して行きます。
このぐらいの揺れであればどれぐらい位置がずれるのかなっていうのが計算できるようになります。
物理の授業みたいになりますのでよろしくお願いします。
加速度、速度、変位の関係がわかる
それぞれの物理量の変換の仕方がわかる
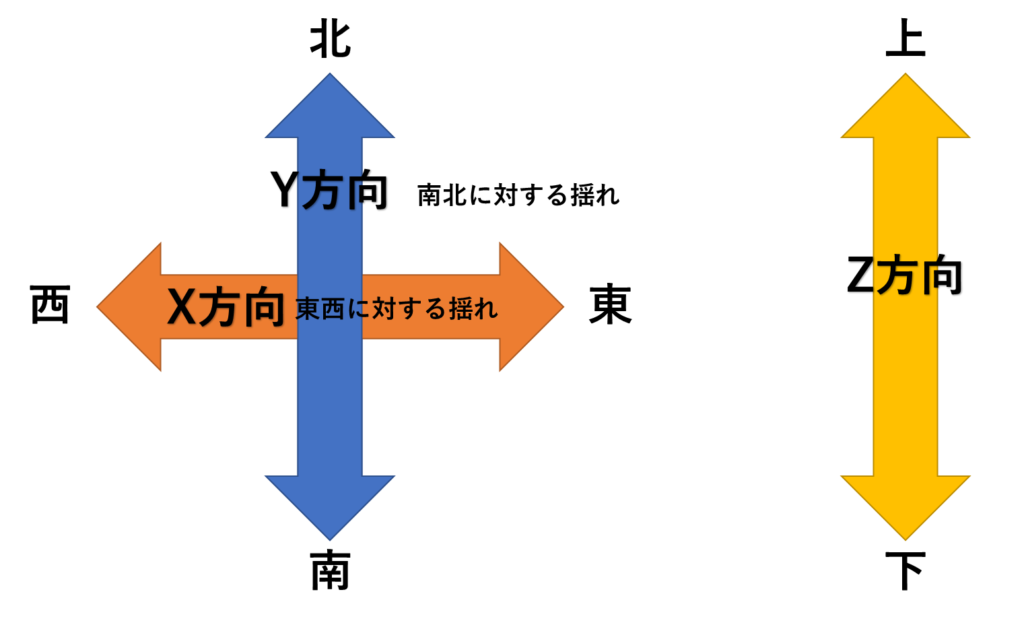
地面の振動の揺れ方にも方向があるって?
まずは振動って何かと言いますと地面の揺れです。
その振動を人間が感じる大きさに数値化したものが振動レベルです。
振動には3種類の方向があります。
一般的に上下に対する揺れが最も大きく感じられます。
次にある時間の振動レベルの変動を示します。
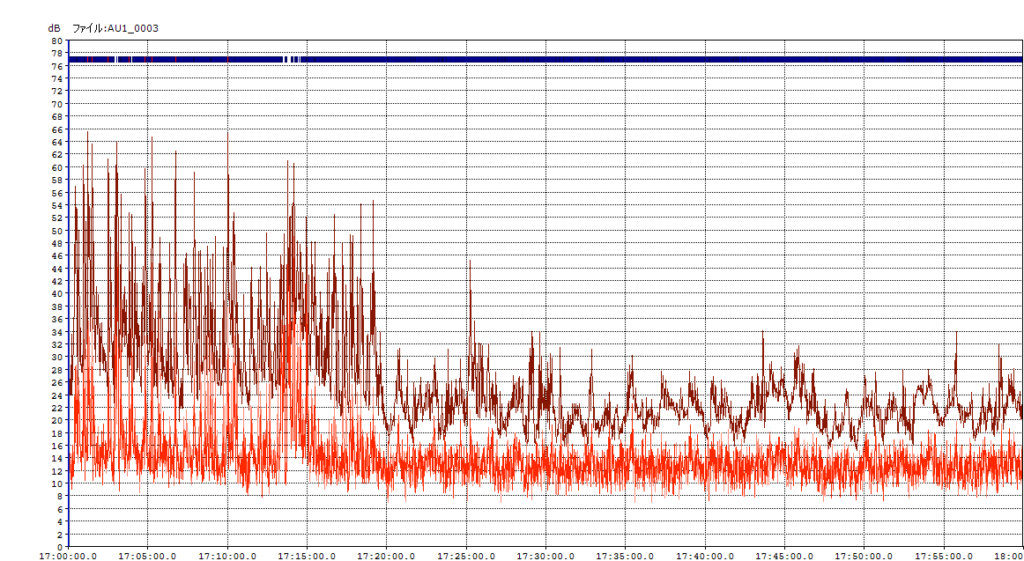
少し分かりにくいので振動レベルが高いところを拡大してみます。
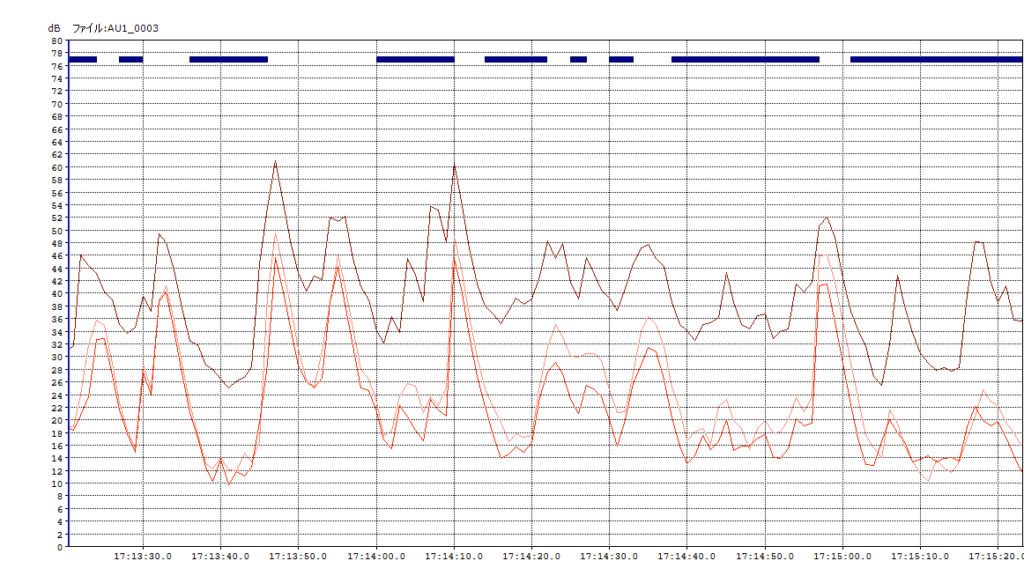
茶色が縦揺れZ 方向になります。
赤色が南北のY方向になります。
橙色が東西のX方向になります。
縦揺れのZ方向が最も高いのは確認できると思います。
このため、一般的に振動レベルと言われるのは、縦揺れの Z 方向が対象になってきます。
振動規制法で使用される振動レベルとは、振動加速度レベルに人間の鉛直方向に おける振動感覚補正を加えたもので、鉛直方向振動加速度レベルと言います。
振動レベルは人間の感じる大きさに補正されています。
この数値を振動感覚補正値です。振動は上下左右ありますが、それぞれ補正値は異なります。
上下振動が最も大きく感じれらるため、鉛直方向の振動レベルとして規制基準などで用いれらています。
また、人体の感じることのできる最小の振動レベルである、振動感覚閾値は、50%の人が感じる振動レベルでおおよそ 60dB、10%の人が感 じる振動レベルでおおよそ 55dB とされています。
加速度って?
加速度の式
振動が揺れであれば、加速度は何かってことになります。
数学で微分・積分って習ったことがあるかも知れません。
文系だと習わないかもしれませんね。
私も昔、この辺で挫折しました。
簡単に言うと速度を細かくしたものです。
1.単位時間に速度が変化する割合。
単位時間とは、例えば1秒などです。
2.速さが次第に増してゆく様子。
3.速さがどの速度で増加していくか
加速度って以下の式で表せます。
速度vを時間tで割ると加速度aが求まるって言うことです。
でもこれって結構、計測には重要なことだったんですね。
振動レベルの数式
例えば、振動レベルって以下の式で表します。
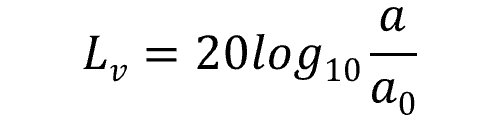
Lv:振動レベル(dB)
a:振動感覚補正後の振動加速度実効値
a0:基準値 10-5m/s2
加速度を基準の加速度で除すことにより得られます。
対数表示するのは数値の表現を見やすくするためです。
この時のa:加速度について考えてみましょう。
加速度は傾きです。
車で速度を上げていくときの上昇程度です。
速度を微分すると加速度になります。
加速度を時間で積分すると速度になります。
速度って
加速度を積分すると速度になります。
逆に距離(変位)を微分すると速度になります。
距離(変位)がy=x2で表される時、距離の式を微分するとy’=2xになります。
さらにy’=2xを微分するとy”=2になります。
加速度は2ですね。
数式で表すと速度って以下の様になります。
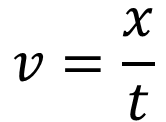
変位って
変位って距離ですね。
振動の中心からのずれを表します。
どれくらいの幅で波の運動を行っているかですね。
これは速度を積分すると得られます。
この変位は、どの様な場合に利用するかといったら、精密加工工場で振動による影響を調べるときに利用します。
例えば、加工精度が〇μmだとします。
周辺の道路で大型車が通った時ある揺れが起こります。
その時の最大の振動レベルから変位を求めます。
これにより、その振動による精密機械の誤差がどれぐらいになるかということを推定することができると考えます。
加速度や速度を測って変位に変換して、加工による不良を推定するかって事ですね。
目安として振動加速度をモニタリングして、ある一定基準を設けておけば、不良品が出た時の原因推定にも役立つかもしれませんね。
振動は地盤の状態によっても伝わり方が変わってきます。それについては以下の記事を参考にしてください。
加速度・速度・変位の変換
どれか1つの物理量がわかると他2つの物理量がわかります。
変換の仕方は下記の通りです。
この時の(cm)と(m)のなどの単位の違いには注意して下さい。

例として
周波数2(Hz)、加速度0.289(cm/s2)の速度と変位と振動レベル(dB)を求めます。
まずは単位の変換です。
0.289(cm/s2)÷100=2.89×10-3(m/s2)
速度 V
V=2.89×10-3(m/s2)÷(2×3.14×2)=2.3×10-4
変位 X
X=2.3×10-4÷(2×3.14×2)=1.9×10-5
振動レベル Lv
20log((2.89×10-3)÷(1×10-5))=49.2(dB)
となりますね。
最後に
ちょっとややこしいかもしれませんが、微分と積分の関係ってわかると楽しいですね。
加速度から速度、変位の変換も出来ると楽しいです。
加速度が分かればどれくらいずれるかを推定できますね。
精密機器などの管理に利用できます。








コメント