距離減衰って
距離減衰ってなにかって言うと離れると小さくなるってことです。
振動だけでなく音でも同じですね。
離れると音が小さくなります。
近くに行くと大きくなります。
この事を距離減衰って言います。
振動も音もエネルギーなんですよね。
離れるってことはエネルギーが薄く広がっていく感じですかね。
距離で振動が減る理由
振動のは以下の様に伝わり予測するものと考えられます。
振動発生源→伝搬経路→受振点
しかし、地盤の土質構成は複雑であり、振動の伝搬の特性をつかむことは容易ではありません。
振動発生源からの伝搬は以下の要素が影響します。
機械と機械基礎の相互作用
機械基礎と地盤との相互作用
上記により土質の内部減衰により指数関数的に減衰していきます。
地盤伝搬の振動は、縦波・横波・表面波と地盤の土質構成により異なります。
減衰傾向は縦波→横波→表面波の順に小さくなると言われています。
幾何減衰
振動源から発生した振動のエネルギーが広い領域に広がり、エネルギーが減っていくために生じる減衰です。
距離の関数のみで減っていくものですね。
この減衰式を示すと下記の通りとなります。
近距離の地盤振動では表面波と実体波が混合して伝搬するものが多くn=0.75に相当する。
| 幾何減衰定数n | 波動 | 伝搬式 | 減衰傾向 |
|---|---|---|---|
| 0.5 | 表面波 | Lvr=Lvr0-10log(r/r0) | -3dB |
| 0.75 | 複合波 表面波と実体波 | Lvr=Lvr0-15log(r/r0) | -4.5dB |
| 1.0 | 実体波 | Lvr=Lvr0-20log(r/r0) | -6dB |
内部減衰
振動のエネルギーが伝搬していく過程で地盤の摩擦などで熱エネルギーなどに変換して減衰するものです。
土質の粘性などによって変わってきます。
土質の性質によって幾何減衰定数も変わってきます。
それらを示したものが下記の通りです。
| 土質 | 幾何減衰定数 n | 減衰勾配 dB/D・D | 波動 |
|---|---|---|---|
| 岩盤 | 1.16 | -7 | 実体波 |
| ローム | 0.83 | -5 | 複合波 |
| シルト | 0.83 | -5 | 複合波 |
| 粘土 | 0.83 | -5 | 複合波 |
| 砂礫 | 0.5 | -3 | 表面波 |
土質の内部減衰式
土質の内部減衰であらわされる減衰量をAd(dB)とすると下記の様になります。
あらわされる

減衰量Adは土質の減衰定位数αが大きいほど大きくなる。
また、振動源と受振源の距離の差が大きいほど大きくなる。
各土質の減衰定数は以下の通りである。
- 粘土:0.02~0.01
- シルト:0.03~0.02
- 関東ローム:0.01
距離による減衰式
振動と土質の内部減衰の関係は以下の通りである。
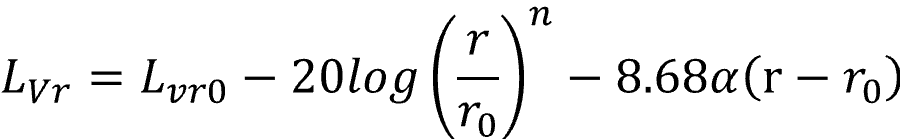
Lvr:受振点での振動レベル(dB)
Lvr0:基準点での振動レベル(dB)
r0:振動源から基準点までの距離(m)
r:振動源から受振点までの距離(m)
n:幾何減衰定数
表面波 0.5
複合波 0.75
実体波 1.0
α:土質の減衰定数
0.04~0.01
V:速度(m/s)
縦波の場合 300~2,000m/s
横波の場合 100~800m/s
地盤が固い方が速くなる
周波数による減衰式
振動の周波数により減衰は異なる。
以下の条件のが減衰は大きくなる。
- 周波数が高くなる
- 波長が短くなる
- 距離が遠くなる
- 土質の損失係数が大きくなる
土質が均一の条件での予測式は下記の通りとなる。
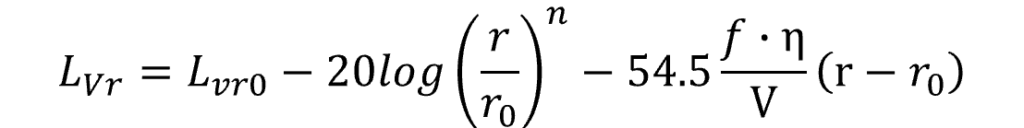
Lvr:受振点での振動レベル(dB)
Lvr0:基準点での振動レベル(dB)
r0:振動源から基準点までの距離(m)
r:振動源から受振点までの距離(m)
n:幾何減衰定数
表面波 0.5
複合波 0.75
実体波 1.0
f:周波数(Hz)
η:土質の損失係数
0.01~0.9
最後に
振動の距離減衰は波動の種類と土質の性質によって変わってきます。
予測するときは、それらを考慮して行うわけですが、どの程度までシミュレーションできるかが重要です。
結局実測値がもっとも正確な気がします。
実測データをもとに補正を行いながら距離減衰を把握することが必要かなって考えます。






コメント